Vigas empotradas y barra de apoyo
Universidad Nacional San Luis Gonzaga de Ica

Lenguaje de programación II
Indice
1. Introducción
2. Objetivos
2.1. Definición
2.2. Explición
2.3. Ejemplo
3. Marco teórico
4. Marco procedimental
5. Conclusión
6.Bibliografía
Introducción:
En este artículo se muestran las fórmulas que se aplican para calcular pendientes y deformaciones en vigas, o sea la flecha máxima y el giro en el apoyo para algunos casos particulares de la curva elástica que se produce en vigas sometidas a cargas.
1. Viga con carga concentrada P a media longitud:
2. Viga con carga concentrada en cualquier longitud
3. Viga con momento aplicado al inicio



Trabajo
En mecánica clásica, se dice que una fuerza realiza trabajo cuando altera el estado de movimiento de un cuerpo. El trabajo de la fuerza sobre ese cuerpo será equivalente a la energía necesaria para desplazarse 11 de manera acelerada.
El trabajo es una magnitud física escalar que se representa con la letra y se expresa en unidades de energía, esto es en julios o joules (J) en el Sistema Internacional de Unidades.
En tal sentido, la “dirección de la fuerza” y la “dirección del movimiento” pueden formar un ángulo (o no formarlo si ambas son paralelas).
Si forman un ángulo (α), debemos incorporar ese dato en nuestra fórmula para calcular el trabajo, para quedar así:
Lo cual se lee: Trabajo = fuerza por coseno de alfa por distancia
Ejemplo:
ACTIVIDAD 1
1.- Un remolcador ejerce una fuerza constante de 4000 N sobre un barco y lo mueve una distancia de 15 m a través del puerto. ¿Qué trabajo realizó el remolcador?
DATOS FÓRMULA CÁLCULOS RESULTADOS
F = 4000N T = Fs T = 4000N X 15m T = 6000N
S =15 m
T = ?

Momento de una fuerza
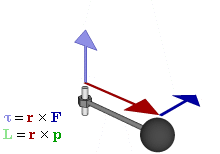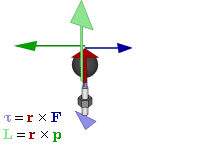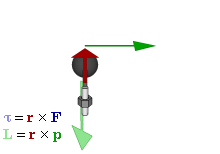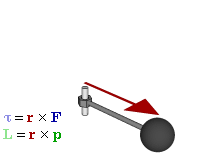
En mecánica newtoniana, se denomina momento de una fuerza (respecto a un punto dado) a una magnitud(pseudo)vectorial, obtenida como producto vectorial del vector de posición del punto de aplicación de la fuerza (con respecto al punto al cual se toma el momento) por el vector fuerza, en ese orden. También se denomina momento dinámico o sencillamente momento.
El momento de una fuerza F aplicada en un punto P con respecto de un punto O viene dado por el producto vectorial del vector OP por el vector fuerza; esto es:
M0 = OP * F = r * F
El momento de una fuerza con respecto a un punto da a conocer en qué medida existe capacidad en una fuerza o sistema de fuerzas para cambiar el estado de la rotación del cuerpo alrededor de un eje que pase por dicho punto.
El momento tiende a provocar una aceleración angular (cambio en la velocidad de giro) en el cuerpo sobre el cual se aplica y es una magnitud característica en elementos que trabajan sometidos a torsión (como los ejes de maquinaria) o a flexión (como las vigas).
Ejemplo:
Se coloca una tuerca con una llave como se muestra en la figura. Si el brazo r es igual a 30 cm y el torque de apriete recomendado para la tuerca es de 30 Nm, ¿cuál debe ser el valor de la fuerza F aplicada?.
Solución:
Σ t = r x F = 0,3 m x F = 30 Nm
Despejando:
0,3 m x F = 30 Nm
F = 30 Nm / 0,3 m
F = 100 N