Indice

1. Introducción

2. Objetivos

2.1. Definición

2.2. Explición

2.3. Ejemplo

3. Marco teórico

4. Marco procedimental

5. Conclusión

6.Bibliografía

Introducción

El ensayo normal a la tensión se emplea para obtener varias características y resistencias que son útiles en el diseño.
Todos los materiales metálicos tienen una combinación de comportamiento elástico y plástico en mayor o menor proporción.
Todo cuerpo al soportar una fuerza aplicada trata de deformarse en el sentido de aplicación de la fuerza.
En el caso del ensayo de tracción, la fuerza se aplica en dirección del eje de ella y por eso se denomina axial.
A escala atómica, la deformación elástica macroscópica se manifiesta como pequeños cambios en el espaciado interatómico y los enlaces interatómicos son estirados.

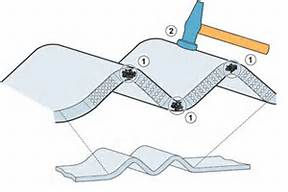
Deformacion por compresión

Si las fuerzas en los extremos de una barra empujan en lugar de tirar, la barra esta en compresión y el esfuerzo es un esfuerzo de compresión. Se define del mismo modo que la deformación por tensión pero, L tiene la dirección opuesta.
En muchas situaciones, los cuerpos experimentan esfuerzos de tensión y compresión al mismo tiempo. Ej: una viga horizontal apoyada en sus extremos se pandea por su propio peso. La parte superior de la viga esta en compresión y la inferior en tensión.

Ejercicio

Un cable de acero de 2.0m de longitud tiene un área transversal de 0.30 cm2 . El cable se cuelga por un extremo de una estructura de soporte y después un torno de 550kg se cuelga del extremo inferior del cable. Determine el alargamiento.

Alargamiento = Deformación . = (9.0 x 10-4 L L0 ) (2.0m) = 0.0018m = 1.8 mm

Esfuerzo de tensión

Deformación por tensión

Es el estiramiento por unidad de longitud; es un numero puro y sin unidades.

Ejemplo:

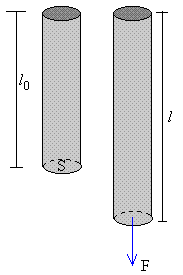
Objeto que inicialmente tiene un área de sección transversal uniforme A y una longitud L0 . Aplicamos fuerzas de igual magnitud F pero direcciones opuestas a los extremos, el objeto no se moverá a la izquierda ni a la derecha. El objeto esta en tensión y todas las partes de la barra se estiran en la misma proporción. El subíndice nos recuerda que las fuerzas actúan en dirección perpendicular a la sección transversal.

Ley de hooke: Historia

Robert Hooke ( 1635 - 1703) fue un científico inglés. Es considerado uno de los científicos experimentales más importantes de la historia de la ciencia, polemista incansable con un genio creativo de primer orden. Sus intereses abarcaron campos tan dispares como la biología, la medicina, la horología (cronometría), la física planetaria, la mecánica de sólidos deformables, la microscopía, la náutica y la arquitectura. Participó en la creación de la primera sociedad científica de la historia, la Royal Society de Londres.

LEY DE HOOKE

La ley de elasticidad de Hooke o ley de Hooke, establece la relación entre el alargamiento o estiramiento longitudinal y la fuerza aplicada. La elasticidad es la propiedad física en la que los objetos con capaces de cambiar de forma cuando actúa una fuerza de deformación sobre un objeto.

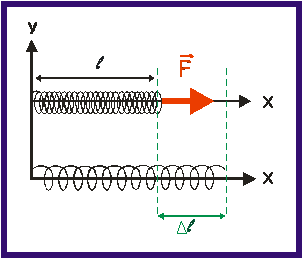
Según la Ley de Hooke, la fuerza aplicada debe ser proporcional a la deformación producida y la constante de proporcionalidad es K, la cual es específica para cada resorte. Esta constante dependerá no sólo del tipo de material del que está hecho el resorte (acero, aluminio, hierro, etc.) sino del diámetro del alambre e incluso de la distancia entre dos vueltas consecutivas de la hélice que forma el resorte y el diámetro de la misma.

La Ley de Hooke para el resorte se escribe:

F = K DL

Microsoft visual c++

Un video sobre la ley de hooke

Bibliografía

R. J. Atkin & N. Fox: An Introduction to the Theory of Elasticity, ed. Dover, 1980.
Baker, Joanne (06 de 2013). 50 cosas que hay que saber sobre física (1ª edición). p. 224. ISBN 978-84-672-5575-1.
Timoshenko, Stephen; Godier J.N. (1951). McGraw-Hill, ed. Theory of elasticity.
Ortiz Berrocal, Luis (1998). McGraw-Hill, ed. Elasticidad. Aravaca (Madrid). pp. 94-96. ISBN 84-481-2046-9.
Olivella, X.; Agelet de Saracibar, C. (2000). «3». En Edicions UPC. Mecánica de Medios Continuos para Ingenieros. Barcelona. pp. 71-75. ISBN 978-84-8301-412-7.